Example 1: Vehicle on Path with Boundaries
In this example, a vehicle is controlled such that it moves along a path.
Contents
The files for this example are found in the package hybrid.examples.vehicle_on_constrained_path :
- initialize.m
- vehicle_on_path.slx
- postprocess.m
The contents of this package are located in Examples\+hybrid\+examples\vehicle_on_constrained_path (clicking this link changes your working directory).
Consider a vehicle modeled by a Dubins vehicle model with state vector \(x=[\xi_1, \xi_2, \xi_3]^\top\) and with dynamics given by \(\dot{\xi_1}=u\cos{\xi_3}\) , \(\dot{\xi_2}=u\sin{\xi_3}\) , and \(\dot{\xi_3}=-\xi_3+r(q)\) . The input \(u\) is the tangential velocity of the vehicle, \(\xi_1\) and \(\xi_2\) describe the vehicle's position on the plane, and \(\xi_3\) is the vehicle's orientation angle. Also consider a switching controller attempting to keep the vehicle inside the boundaries of a track given by \(\{(\xi_1,\xi_2):-1\leq\xi_1\leq1\}\) . A state \(q \in \{1,2\}\) is used to define the modes of operation of the controller. When \(q=1\) , the vehicle is traveling to the left, and when \(q=2\) , the vehicle is traveling to the right. A logic variable \(r\) is defined in order to steer the vehicle back inside the boundary. The state of the closed-loop system is given by \(x := [\xi^\top\ q]^\top\) .
Mathematical Model
A model of such a closed-loop system is given by
\[ \begin{array}{l} f(x,u) := \left[\begin{array}{c} u\cos(\xi_3) \\ u\sin(\xi_3)\\ -\xi_3+r(q) \\ 0 \end{array}\right] + \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \end{array}\right] u, \quad r(q) := \left\{\begin{array}{cc} \frac{3\pi}{4} & \textrm{if } q=1 \\ \frac{\pi}{4} & \textrm{if } q=2 \\ \end{array}\right. \\ \\ C := \{(\xi, q, u)\in \mathbb{R}^{3}\times\{1,2\}\times \mathbb{R}\mid (\xi_1 \leq 1,\ q = 2) \textrm{ or } (\xi_1 \geq -1,\ q=1)\}, \\ \\ g(x,u) := \left\{\begin{array}{ll} \left[\begin{array}{c} \xi \\ 2 \end{array}\right] & \textrm{if } \xi_1\leq-1,\ q=1 \\ \\ \left[\begin{array}{c} \xi \\ 1 \end{array}\right] & \textrm{if } \xi_1\geq 1,\ q=2, \end{array} \right. \\ \\ D := \{(\xi, q, u)\in \mathbb{R}^{3}\times\{1,2\} \times \mathbb{R} \mid(\xi_1 \geq 1,\ q = 2) \textrm{ or } (\xi_1 \leq -1,\ q=1)\} \end{array}\]
Simulink Model
The Simulink blocks for the hybrid system in this example are included below.
flow map f block
function xdot = f(x, u)
% Flow map for Vehicle Traveling on a Track
% State
xi3 = x(3); % Orientation angle
q = x(4);
% q = 1 --> going left
% q = 2 --> going right
if q == 1
r = 3*pi/4;
elseif q == 2
r = pi/4;
else
r = 0;
end
xi1dot = u*cos(xi3); % Tangential velocity in x-direction
xi2dot = u*sin(xi3); % Tangential velocity in y-direction
xi3dot = -xi3 + r; % Angular velocity
qdot = 0;
xdot = [xi1dot; xi2dot; xi3dot; qdot];
end
flow set C block
function inC = C(x, u)
% Flow set for Vehicle Traveling on a Track
% State
xi1 = x(1); %x-position
q = x(4);
% q = 1 --> going left
% q = 2 --> going right
if ((xi1 < 1) && (q == 2)) || ((xi1 > -1) && (q == 1)) % flow condition
inC = 1; % report flow
else
inC = 0; % do not report flow
end
end
jump map g block
function xplus = g(x, u)
% Jump map for Vehicle Traveling on a Track
% State
xi = x(1:3);
% q = 1 --> going left
% q = 2 --> going right
q = x(4);
if ((xi(1) >= 1) && (q == 2)) || ((xi(1) <= -1) && (q == 1))
qplus = 3-q;
else
qplus = q;
end
xplus = [xi; qplus];
end
jump set D block
function inD = D(x, u)
% Jump set indicator function for Vehicle Traveling on a Track
% State
xi1 = x(1); %x-position
% q = 1 --> going left
% q = 2 --> going right
q = x(4);
if ((xi1 >= 1) && (q == 2)) || ((xi1 <= -1) && (q == 1)) % jump condition
inD = 1; % report jump
else
inD = 0; % do not report jump
end
end
Example Output
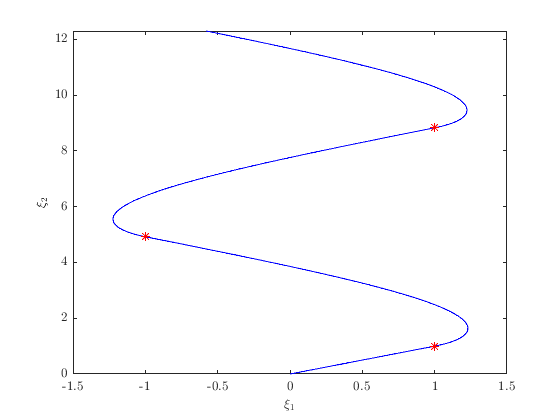
A solution to the system above is plotted below with initial position \((\xi_1,\xi_2)=(0,0)\) , initial orientation angle \(\xi_3=\frac{\pi}{4}\) radians, T=15 , J=10 , and rule=1 .
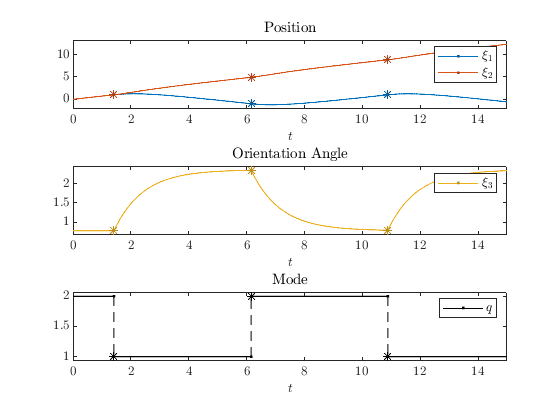
The following plot depicts the trajectory of the vehicle.