Example 2: Synchronization of Two Fireflies
In this example, two hybrid subsystems in Simulink are used to model a pair of fireflies that exhibit synchronization of their flashes.
Contents
The files for this example are found in the package hybrid.examples.fireflies :
- initialize.m
- fireflies.slx
- postprocess.m
The contents of this package are located in Examples\+hybrid\+examples\fireflies (clicking this link changes your working directory).
Consider a biological example of the synchronization of two fireflies flashing. The fireflies can be modeled mathematically as periodic oscillators which tend to synchronize their flashing until they are flashing in phase with each other. A state value of \(\tau_i=1\) corresponds to a flash, and after each flash, the firefly automatically resets its internal timer (periodic cycle) to \(\tau_i=0\) . The synchronization of the fireflies can be modeled as an interconnection of two hybrid systems because every time one firefly flashes, the other firefly notices and jumps ahead in its internal timer \(\tau\) by \((1+\varepsilon)\tau\) , where \(\varepsilon\) is a biologically determined coefficient. This happens until eventually both fireflies synchronize their internal timers and are flashing simultaneously.
Mathematical Model
Each firefly can be modeled as a hybrid system given by
\[\begin{array}{ll} f_i(\tau_i,u_i) := 1, & C_i := \{(\tau_i,u_i)\in \mathbb{R}^{2}\mid 0 \leq \tau_i \leq 1\}\cap \{(\tau_i,u_i)\in \mathbb{R}^{2}\mid 0 \leq u_i \leq 1\} \\ g_i(\tau_i,u_i) := \left\{ \begin{array}{ll} (1+ \varepsilon)\tau_i & (1+\varepsilon)\tau_i<1 \\ 0 & (1+\varepsilon)\tau_i\geq 1 \end{array} \right. & D_i := \{(\tau_i,u_i)\in \mathbb{R}^{2} \mid \tau_i = 1\} \cup \{(\tau_i,u_i)\in \mathbb{R}^{2}\mid u_i = 1\}. \end{array}\]
Simulink Model
The following diagram shows the Simulink model of two interconnected firefly subsystems.
The interconnection diagram for this example is simpler than in the previous example link because now no external inputs are being considered. The only event that affects the flashing of a firefly is the flashing of the other firefly. The interconnection diagram can be seen here:

The Simulink blocks for the hybrid system in this example are included below.
flow map f block
function taudot = f(tau, u)
% Flow map for firefly.
taudot = 1;
end
flow set C block
function inC = C(tau, u)
% Flow set indicator function for firefly.
if ((tau > 0) && (tau < 1)) || ((u > 0) && (u <= 1)) % flow condition
inC = 1; % report flow
else
inC = 0; % do not report flow
end
end
jump map g block
function tauplus = g(tau, u, e)
% Jump map for firefly.
if (1+e)*tau < 1
tauplus = (1+e)*tau;
elseif (1+e)*tau >= 1
tauplus = 0;
else
tauplus = tau;
end
end
jump set D block
function inD = D(tau, u)
% Jump set indicator function for firefly.
if (u >= 1) || (tau >= 1) % jump condition
inD = 1; % report jump
else
inD = 0; % do not report jump
end
end
Example Output
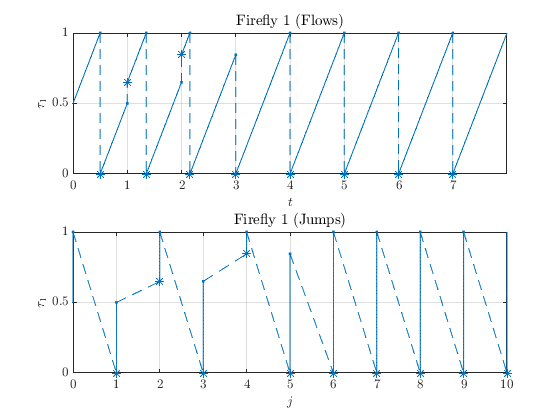
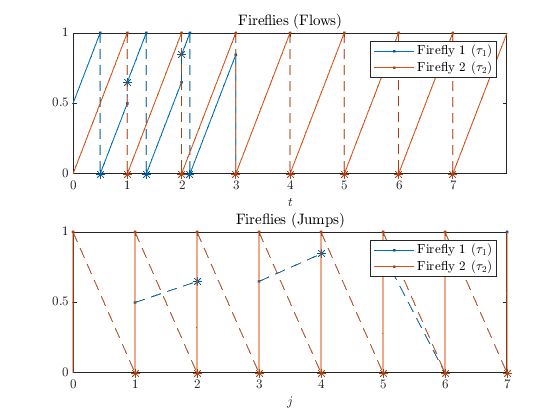
A solution to the interconnection of hybrid systems \(\mathcal{H}_1\) and \(\mathcal{H}_2\) with T=15, J=15, rule = 1 , \(\varepsilon=0.3\) is shown below. The projection onto \(t\) is shown in the top subplot and the projection onto \(j\) is shown on the bottom.
This simulation reflects the expected behavior of the interconnected hybrid systems. Initially, the fireflies flash out of phase with one another but eventually synchronize to flash in sync.
The isolated solutions to the hybrid subsystems \(\mathcal{H}_1\) and \(\mathcal{H}_2\) are are shown below.